Клиническое испытание и клиническое исследование: сходство и различие
Г. П. ТИХОВА
Республиканский перинатальный центр, Петрозаводск, Республика Карелия
Термин «доказательная медицина», столь популярный в настоящее время, распространяется на широкий круг проблем как практической, так и научной областей медицинского знания. Это фактически новый, более строгий формализованный подход к получению, оценке и применению медицинской информации, который был озвучен еще в XIX веке, но получил мощный толчок развития лишь около десяти лет назад, благодаря невероятной скорости накопления новых данных и возможности их быстрой обработки. Первыми разделами медицинского знания, которые реально столкнулись с проблемой четкой формализации алгоритма принятия решений, были клиническая эпидемиология и клиническая фармакология. Однако вскоре другие специальности также подошли вплотную к необходимости решения подобных задач, и во многом критерии оценки и формализованные алгоритмы постановки эксперимента, выработанные при решении конкретных задач эпидемиологии и фармакологии, могли служить готовым решением аналогичных проблем в других областях медицины. Несмотря на свой малый возраст, доказательная медицина вполне достойна того, чтобы о ее целях, задачах и методах писались монографии. В наших публикациях мы затронем лишь одну небольшую проблему, а именно – поговорим о планировании научного исследования, о различных дизайнах (планах) экперимента и исследования, а также о методах обработки полученных в ходе этого исследования данных и о степени доказанности выводов, сделанных на основе полученных результатов.
Эксперимент или исследование, доказательство или поиск?
Интуитивно понятно, что все научные изыскания можно условно разделить на две категории: одни проводятся для выдвижения и формулирования гипотез, другие для проверки (доказательства или опровержения) этих гипотез. Для проверки гипотез (а также новых препаратов, новых методов лечения и т.д.) проводятся клинические испытания , как правило, это рандомизированные контролируемые двойные или простые слепые испытания , имеющие множество нюансов и разновидностей, а также названий, с которыми мы познакомимся несколько позже. Клинические исследования отличаются от них тем, что их результатом, как правило, является некоторая гипотеза, новый научный факт или новый взгляд на уже известные факты, иными словами, новое знание, которое формулируется с определенной долей уверенности (как статистической, так и клинической) и которое требует верификации (подтверждения или опровержения) с помощью клинического испытания, если таковое возможно и необходимо. Отметим сразу же, что такое разделение вовсе не означает ущербности исследований по сравнению с испытаниями или наоборот, они просто служат разным целям. Очень важно различать клинические испытания и клинические исследования именно по их основной цели: клинические исследования, как правило, проводятся с целью получить новое знание (гипотезу, факт, теорию), в то время как клинические испытания не привносят ничего нового, они лишь подтверждают или опровергают уже известную гипотезу, факт, теорию, то есть меняют степень уверенности по отношению к уже полученному знанию. Для проведения клинических испытаний разработана жестко регламентированная методология, доведенная практически до схем и конкретных алгоритмов принятия решений. Важно отметить, что она лишь частично и далеко не всегда может быть экстраполирована на методологию проведения клинического исследования, именно потому, что клиническое испытание и клиническое исследование служат разным целям и проводятся на разных стадиях формирования нового знания. Очень четко и лаконично определил разницу между клиническим испытанием и клиническим исследованием К.П.Воробьев (Луганская областная клиническая больница), в своей статье «Доказательная медицина, научные исследования и клиническая практика» он пишет: «Разделение понятий исследование и испытание несет целый ряд важных для науки и практики следствий. Главные из них заключаются в том, что исследование - это этап получения нового знания, который носит личностный характер и является предметом научных изысканий, а испытание это этап верификации нового гипотетического знания, который носит безличностный (общественный) характер и выполняется по заранее разработанному протоколу проведения и оценки испытания.» И чуть далее тот же автор резонно замечает: «Существует мнение, что серьезные научные журналы публикуют только результаты правильно организованных рандомизированных клинических испытаний. Это грубое заблуждение. Если все кинутся проверять гипотезы, то кто же их будет создавать? »
Итак, клиническое исследование и клиническое испытание – это вовсе не разные названия одного и того же процесса. Клинические исследования и клинические испытания кардинальным образом отличаются друг от друга:
целью: клиническое исследование проводится с целью получения нового знания, которое верно с некоторой (не всегда численно определенной) вероятностью, тогда как клиническое испытание призвано подтвердить или опровергнуть новое знание с вероятностью, выше заранее заданного допустимого порога;
методологией: цель клинического испытания почти однозначно определяет его дизайн, тогда как дизайн клинического исследования в значительной степени зависит от опыта и знаний исследователя;
фазой проведения: клиническое исследование, и часто не одно, всегда предшествует клиническому испытанию, так как сначала нужно что-то обнаружить, и лишь затем можно задаваться вопросом: верно это или нет.
Приведем примеры из публикаций, размещенных на нашем сайте.
1. В разделе «Анналы->Анестезиология->Анестезиология в акушерстве и гинекологии» можно найти публикацию Г.Филиповича и Е.Шифмана «Анестезия операции кесарева сечения при многоплодной беременности». По своему дизайну это исследование является ретроспективным обсервационным исследованием серий случаев с заданными параметрами, иначе говоря, это – клиническое исследование, но не испытание. Это исследование позволяет свести сложную проблему доказательства безопасности спинальной анестезии при операции КС в случае многоплодной беременности к обзору нескольких интегральных показателей и сравнению их с таковыми при общей анестезии, что и позволяет подтвердить эту гипотезу. Насколько репрезентативна выборка, по которой произведен статистический анализ? Объем ее вполне достаточен, чтобы отразить тенденции, характерные для исследуемой популяции, но рандомизация для ее выделения из генеральной совокупности не проводилась, поэтому формально она не защищена от ошибок смещения. Но насколько реально возникновение в данном исследовании таких фатальных смещений, которые бы в корне могли поменять интегральную статистическую картину? С позиции специалиста, знакомого с исследуемой проблемой, это очень маловероятно. Кроме того, данное исследование является ярким примером ситуации, когда рандомизация, в формальном ее понимании, может оказаться невозможной, поскольку как у спинальной анестезии, так и у общей анестезии имеются абсолютные противопоказания, не позволяющие произвольно относить пациенток к одной или другой группе. Данное исследование является характерным примером пилотного клинического исследования, результатом которого является гипотеза, подтвержденная с определенной степенью статистической вероятности и экспертной оценки результатов. Конечно, можно попытаться в дальнейшем провести классическое клиническое испытание данного метода в заданных условиях, но, как было указано выше, в процессе его проведения могут возникнуть непреодолимые препятствия. Всегда стоит взвесить объем трудозатрат и получаемый в результате уровень уточнения уже известных фактов. Возможно, картина и так достаточно ясна и не стоит биться за лишние тысячные в уровне значимости.
2. С характерным примером клинического испытания можно познакомиться в статье «0,2% ропивакаин и левобупивакаин обеспечивают равно эффективную эпидуральную анальгезию в родах», которая опубликована на нашем сайте в «Школе регионарной анестезии », раздел «Публикации». Отличие ее от предыдущей работы состоит, прежде всего, в методике формирования выборки данных для анализа и последовательности действий. Это испытание является рандомизированным (пациенты случайным образом включались в одну из двух групп) проспективным (сначала были поставлены цели исследования, а потом уже набирались данные) клиническим испытанием. Как отмечено в комментарии к статье подобные испытания уже проводились и ранее, и данная работа не несет новой информации, но лишь усиливает уверенность в правильности предположения о равном анальгетическом эффекте 0,2% ропивакаина и левобупивакаина в родах и уточняет некоторые детали.
Эти два примера приблизительно демонстрируют основные отличительные особенности клинического исследования и клинического испытания.
Репрезентативная выборка и генеральная совокупность.
Объединяет клинические исследования и испытания то, что обычно и в том, и в другом случае исследуемая генеральная совокупность представлена выборкой, на которой и производятся все необходимые действия. Но что такое генеральная совокупность, и почему мы имеем право экстраполировать на нее выводы, полученные в ходе исследования выборки? Генеральная совокупность – это вся популяция пациентов, которая является предметом исследования. Она может быть как очень велика, так и настолько малочисленна, что делать из нее выборку не имеет никакого смысла. В последнем случае исследуется непосредственно сама генеральная совокупность, но такие случаи крайне редки. Как правило, популяция, представляющая интерес для исследования, столь велика, что объять ее целиком в исследовании не представляется возможным, поэтому из нее делают выборку, которая является своего рода представителем этой генеральной совокупности. Насколько свойства этой выборки реально отражают (представляют) свойства всей генеральной совокупности, зависит от ее репрезентативности, т.е. представительности, иными словами, от того каким образом мы формировали выборку для исследования. Рассмотрим эти три понятия: генеральная совокупность, выборка и репрезентативность на следующем простом примере.
Допустим, мы исследуем величину массы тела в килограммах у жителей деревни Х, число которых составляет 20 человек. Поскольку нас интересуют жители только этой деревни, то генеральной совокупностью в данном случае будет все население деревни Х. В результате последовательного взвешивания всех жителей мы получили следующие значения, показанные в таблице 1 отображенные на рисунке 1.
Таблица 1. Данные всех жителей, необходимые для исследования.
Номер п/п |
Вес (кг) |
Пол |
1 |
77 |
муж |
2 |
77 |
муж |
3 |
74 |
муж |
4 |
67 |
жен |
5 |
65 |
жен |
6 |
75 |
муж |
7 |
62 |
муж |
8 |
81 |
муж |
9 |
65 |
муж |
10 |
62 |
жен |
11 |
56 |
жен |
12 |
65 |
жен |
13 |
65 |
жен |
14 |
84 |
муж |
15 |
58 |
жен |
16 |
66 |
муж |
17 |
61 |
муж |
18 |
61 |
муж |
19 |
70 |
жен |
20 |
60 |
жен |
| Средний вес жителей деревни Х = 67,6 | ||
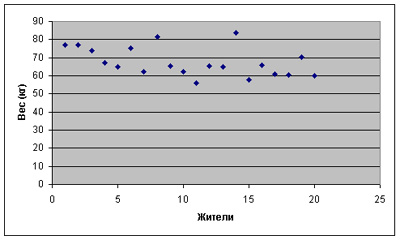 |
| Рис.1 Значения веса всех членов исследуемой популяции (генеральной совокупности) |
Нетрудно подсчитать среднее значение массы тела жителей деревни Х, оно равно 67,6 кг. Заметьте, что это среднее значение является совершенно точным числом, поскольку мы обследовали всю интересующую нас популяцию. Это значение также является неотъемлемым свойством изучаемой генеральной совокупности на момент исследования. Предположим, что по каким-то причинам мы не можем взвесить всех жителей деревни и должны выбрать только 10 из 20 человек. Поскольку нам доступна лишь половина информации, мы не можем рассчитывать получить точное среднее значение, как это было при исследовании всей популяции. Каким бы методом мы ни пользовались для выделения выборки объемом 10 человек, наше выборочное среднее значение будет лишь приближенной оценкой реального среднего значения, имеющего место в данной популяции. Рассмотрим несколько вариантов таких выборок и проследим за тем, насколько сильно отклоняется выборочное среднее от среднего генеральной совокупности. Вначале перенумеруем всех жителей деревни Х в произвольной последовательности. Далее сделаем следующее:
1 вариант выборки . Из всех жителей деревни выберем тех, которые получили нечетные номера. Значения, включенные в эту выборку, представлены в таблице 2.
Таблица 2. Данные выборки 1
Номер п/п |
Вес (кг) |
Пол |
1 |
77 |
муж |
3 |
74 |
муж |
5 |
65 |
жен |
7 |
62 |
муж |
9 |
65 |
муж |
11 |
56 |
жен |
13 |
65 |
жен |
15 |
58 |
жен |
17 |
61 |
муж |
19 |
70 |
жен |
| Средний вес = 65,3 | ||
2 вариант выборки . Отберем тех жителей, которые имеют первые десять номеров. Значения, включенные в эту выборку, представлены в таблице 3.
Таблица 3 . Данные выборки 2
Номер п/п |
Вес (кг) |
Пол |
1 |
77 |
муж |
2 |
77 |
муж |
3 |
74 |
муж |
4 |
67 |
жен |
5 |
65 |
жен |
6 |
75 |
муж |
7 |
62 |
муж |
8 |
81 |
муж |
9 |
65 |
муж |
10 |
62 |
жен |
| Средний вес = 70,6 | ||
3 вариант выборки . Датчиком случайных чисел в диапазоне от 1 до 20 выделим десять номеров тех жителей, вес которых будет включен в исследуемую выборку. Данные этой выборки представлены в таблице 4.
Таблица 4. Данные выборки 3.
Номер п/п |
Вес (кг) |
Пол |
1 |
77 |
муж |
2 |
77 |
муж |
5 |
65 |
жен |
8 |
81 |
муж |
11 |
56 |
жен |
12 |
65 |
жен |
13 |
65 |
жен |
16 |
66 |
муж |
17 |
61 |
муж |
20 |
60 |
жен |
| Средний вес = 67,3 | ||
Теперь сравним выборочные средние значения с точным средним генеральной совокупности (таблица 5, рисунок 2 ).
Таблица 5. Сравнение выборочных оценок среднего веса, рассчитанных по разным выборкам
Ген. совокупность |
Выборка 1 |
Выборка 2 |
Выборка 3 |
|
Средний вес (кг) |
67,6 |
65,3 |
70,6 |
67,3 |
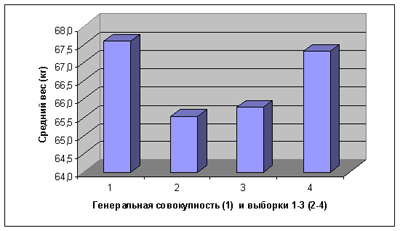 |
| Рис. 2. Сравнение выборочных оценок среднего веса, рассчитанных по разным выборкам, выделенным из одной и той же популяции |
Мы видим, что две первые оценки несколько отклоняются от реального среднего значения, а наиболее близкой к нему является оценка, полученная при обработке третьей выборки. Обратим внимание, что первые две выборки мы сформировали так называемыми псевдослучайными методами, а третью – с помощью датчика случайных чисел, т.е. действительно случайным образом отбирая участников исследования. Такой отбор участников исследования называется рандомизацией. Рандомизированная выборка достаточного объема является, как правило, репрезентативной, т.е. она имеет приблизительно те же свойства, что и генеральная совокупность, из которой она взята и все статистики, рассчитанные на ее основе, являются наиболее вероятными приближенными оценками соответствующих статистик генеральной совокупности. Вот почему обработав данные такой выборки и получив какие-то заключения на ее основе, мы в праве с определенной вероятностью экстраполировать эти выводы на всю генеральную совокупность. Но что происходит, если наша выборка не рандомизирована? И почему две первые выборки из нашей исследуемой популяции дали отклонения в оценке среднего значения? Попробуем разобраться сразу с обеими выборками. Во-первых, они формировались без применения процедур рандомизации. Мы просто решали, какой житель будет включен в исследование, а какой нет. Очень часто при такой процедуре выбора сознательно или несознательно исследователь выбирает наиболее «интересных» пациентов, т.е. имеющих какие-то особенности, формируя, таким образом, интегральные свойства выборки, отличные от свойств генеральной совокупности. Выборка уже не отражает свойств исследуемой популяции, она смещена под воздействие воли исследователя. Если даже вмешательство профессионального интереса исследователя сведено к минимуму, то простое назначение и отбор участников с номерами, подчиняющимися какой-то закономерности, может также привести к смещенной выборке, поскольку представители популяции, обладающие редко встречающимися свойства могут оказаться компактно сгруппированными нашей нумерацией и попасть в выборку в количестве, превышающем характерное для этой популяции. Примером тому являются две первые выборки нашего гипотетического исследования. Чтобы разобраться, в чем дело, отметим пол всех жителей исследуемой популяции и подсчитаем среднее значение веса в группах женщин и мужчин отдельно. Результаты представлены в таблице 6.
Таблица 6. Средние значения веса в группах мужчин и женщин,
рассчитанные по всей исследуемой популяции
Пол |
Средний вес (кг) |
Кол-во в группе (%) |
Мужчины |
71,1 |
11 (55) |
Женщины |
63,1 |
9 (45) |
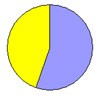
Заметим, что женщины этой деревни в среднем несколько легче мужчин и количество их меньше. Теперь с этой же точки зрения посмотрим на наши выборки и сравним их с генеральной совокупностью ( таблица 7, рисунок 3 ).
Таблица 7. Сравнение выборочных оценок соотношения мужчин и женщин в разных выборках
Вся популяция |
Выборка 1 |
Выборка 2 |
Выборка 3 |
|
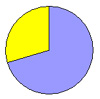
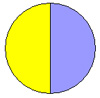
| Соотношения мужчин/женщин (%) | 55/45 |
50/50 |
70/30 |
50/50 |
 |
 |
 |
 |
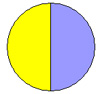
| Вся популяция | Выборка 1 | Выборка 2 | Выборка 3 |
 |
|||
| Рис. 3.Сравнение выборочных оценок соотношения мужчин и женщин в разных выборках | |||
Мы видим, что в первой выборке количество женщин и мужчин у нас получилось равным, из чего мы могли бы сделать ложный вывод, что и вся популяция по признаку пола делится ровно пополам. Кроме того, можно заметить, что более тяжелые мужчины попросту не попали в наше исследование. Следствием всего этого является то, что оценка среднего веса жителей деревни Х оказалась несколько заниженной. Во второй выборке соотношение мужчин к женщинам еще сильнее отличается от реальности, в результате чего в выборку попали в основном «тяжелые» жители и оценка превысила реальное значение. Наконец, в третьей выборке, несмотря на то, что соотношение по полу, также несколько отличается от реального, в выборку, благодаря процедуре случайного отбора, были включены как характерные, так и необычно тяжелые и легкие индивидуумы в таких пропорциях, которые имеют место и в генеральной совокупности. Это привело к тому, что оценка, полученная при обработке данных третьей выборки, наиболее близка к реальному значению.
Этот простой пример демонстрирует важность выделения из генеральной совокупности именно репрезентативной выборки, т.е. наиболее приближенной по своим свойствам к исследуемой популяции. И волшебной палочкой, помогающей осуществить это, служит процедура рандомизации или, иными словами, отбор методом случайных чисел. Позже мы подробно остановимся на этих методах, а сейчас уточним еще одну проблему, которая может помешать формированию репрезентативной выборки. В таблице 8 показана выборка, выделенная из той же популяции жителей методом случайного отбора, но объем ее равен лишь трем.
Таблица 8. Выборка малого объема
Номер п/п |
Вес (кг) |
Пол |
8 |
81 |
муж |
10 |
62 |
жен |
11 |
56 |
жен |
| Средний вес = 66,3 Соотношение муж/жен = 33%/67% |
||
Мы видим, что, во-первых, соотношение мужчин и женщин в этой выборке грубо нарушено по сравнению с реально существующим в популяции, и, во-вторых, оценка занижена, несмотря на то, что мы пользовались для отбора участников методом рандомизации. Почему это произошло? На степень репрезентативности выборки оказывает огромное влияние не только метод, которым она формировалась, но и ее объем. Чем меньше объем выборки, тем большее влияние на ее статистики оказывает каждый член этой выборки, а значит, те нехарактерные данные, которые могут попасть в нее из генеральной совокупности. Иными словами, выборка может быть смещена за счет слишком сильного влияния тех членов генеральной совокупности, которые в самой популяции имеют незначительный вес. Так произошло в нашей хоть и рандомизированной, но малочисленной выборке, где более «легкие» женщины составили большинство и таким образом сместили оценку среднего ниже реального значения. В случае клинического испытания определение достаточного объема выборки доведено до алгоритма и конкретных расчетов при разработке протокола, но для клинического исследования эта задача не так проста и очевидна. Очень упрощенно, в первом приближение, можно сказать, что чем больше объем выборки, тем она репрезентативнее, а также точнее и выборочные оценки параметров генеральной совокупности, но это не значит, что всегда необходимо стремиться к гигантским массивам данных. Начиная с некоторого значения N (объема выборки) улучшение ее репрезентативности, а также статистических оценок будет незначительным и просто несопоставимым с огромными затратами на обработку увеличивающегося потока данных. При проведении клинического исследования также не может быть принято безоговорочно и требование обязательного применения рандомизации при формировании выборки. К этому надо стремиться, но в разумных пределах, поскольку зачастую рандомизация в клиническом исследовании бывает невозможна, а иногда и нежелательна. Однако это ни в коем случае не означает, что результаты такого исследования не достоверны и не заслуживают внимания. При грамотной статистической и клинической оценке достоверности результатов, а также вероятности смещения выборки под воздействием неучтенных известных факторов, такое исследование может стать стартом для новых идей и гипотез. Примером такого исследования является статья «Информативность биохимических показателей плазмы при гестозах», которую можно найти на нашем сайте в разделе «Анналы->Интенсивная терапия->Преэклампсия-эклампсия».
Итак, в клинических испытаниях и клинических исследованиях предметом исследования является некая генеральная совокупность (популяция) с характерными свойствами и численными параметрами, которая представлена репрезентативной выборкой, т.е. выборкой приближенно отражающей эти свойства и параметры.
Именно на этой выборке производятся все процедуры и расчеты, на основе которых с некоторой вероятностью делаются заключения относительно всей генеральной совокупности. Эта вероятность может быть выражена как статистической оценкой (клинические испытания и клинические исследования), так и экспертной оценкой (клинические исследования).
Для обеспечения репрезентативности выборки, она должна быть достаточного объема и формироваться из исследуемой генеральной совокупности методами рандомизации.
В клинических исследованиях методы рандомизации не всегда имеют место при формировании выборки. Это вполне допустимо при грамотной оценке возможного смещения нерандомизированной выборки относительно исследуемой генеральной совокупности.

